
コンピュータを用いて数値的に問題を解くときに必要となる,いくつかの基本的な数値計算アルゴリズムを講義する.線形計算,常微分方程式の数値積分,高速フーリエ変換,有限要素法等に関するアルゴリズムの構成,特徴,使い方を説明する.実際にプログラミング言語でプログラムを書き,アルゴリズムを理解し,運用することを目指す.
| 第1週 | 4/ 9 | 数値計算とは: 解析解,数値解 | |
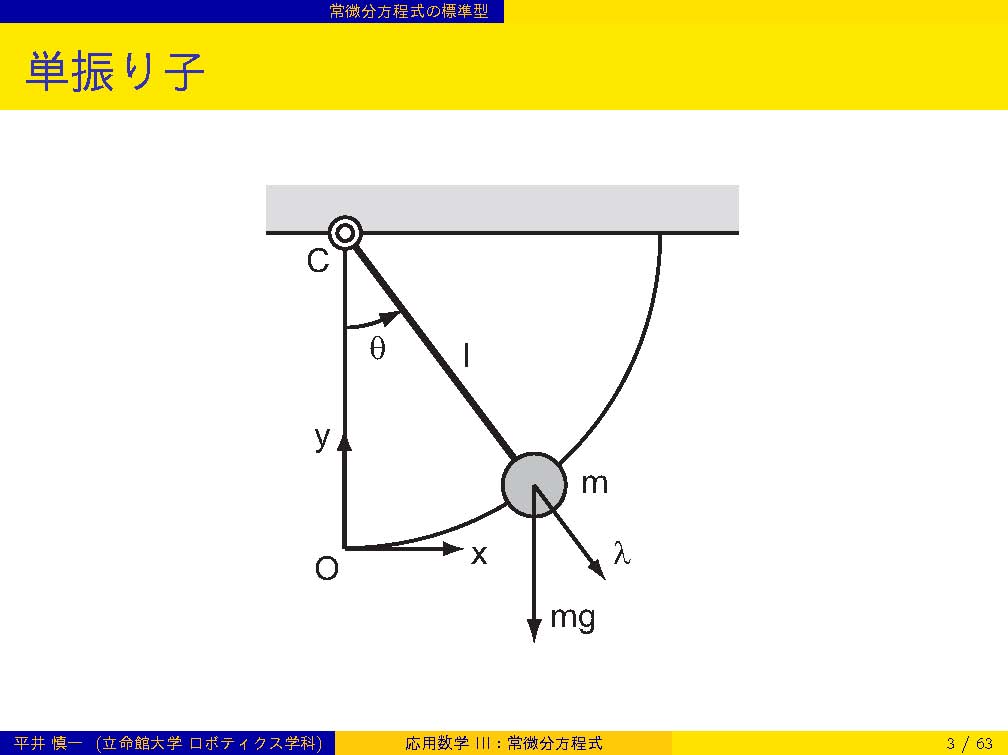
| 第2週 | 4/16 | 常微分方程式: 常微分方程式の標準形,Euler法,Heun法,Runge-Kutta法 | |
| 第3週 | 4/23 | 常微分方程式: Runge-Kutta-Fehlberg法,ホロノミック制約,制約安定化法(CSM) | |
| 第4週 | 4/30 | 連立一次方程式: ガウスの消去法,LU分解,三角行列の性質,コレスキー分解 | |
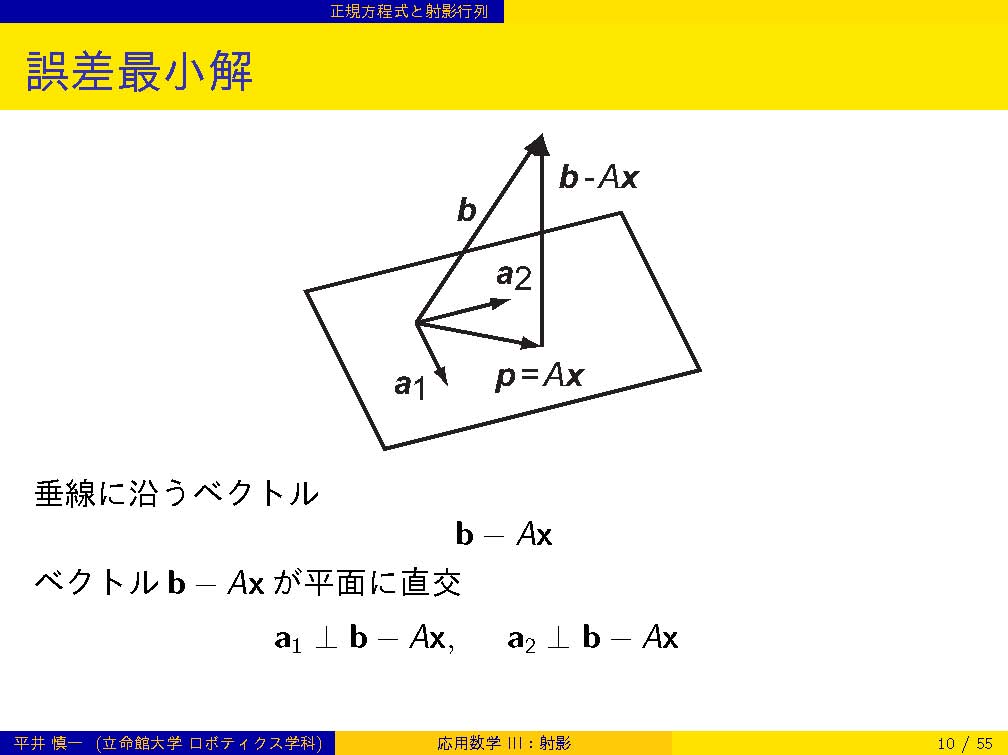
| 第5週 | 5/ 7 | 射影: 誤差最小解,射影行列,グラム・シュミットの直交化,QR分解 | |
| 第6週 | 5/21 | (小テスト) 常微分方程式,連立一次方程式 | |
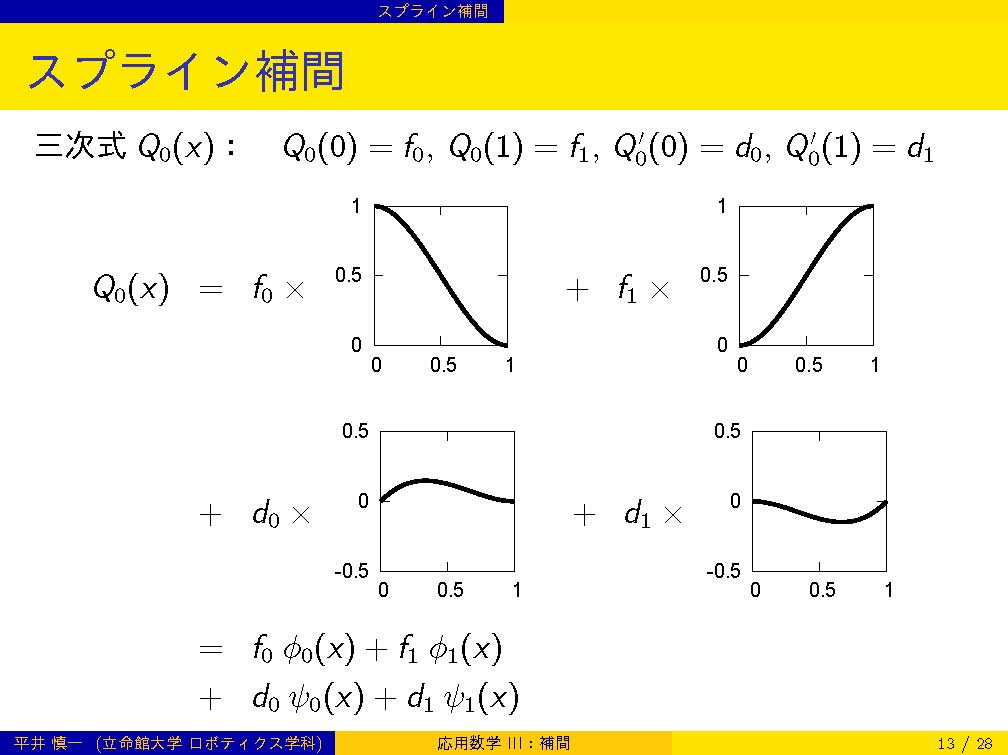
| 第7週 | 5/26 | 補間: 区分線形補間,スプライン補間 | |
| 第8週 | 5/28 | 変分原理: ラグランジアン,制約付きラグランジアン,ラグランジュの運動方程式 | |
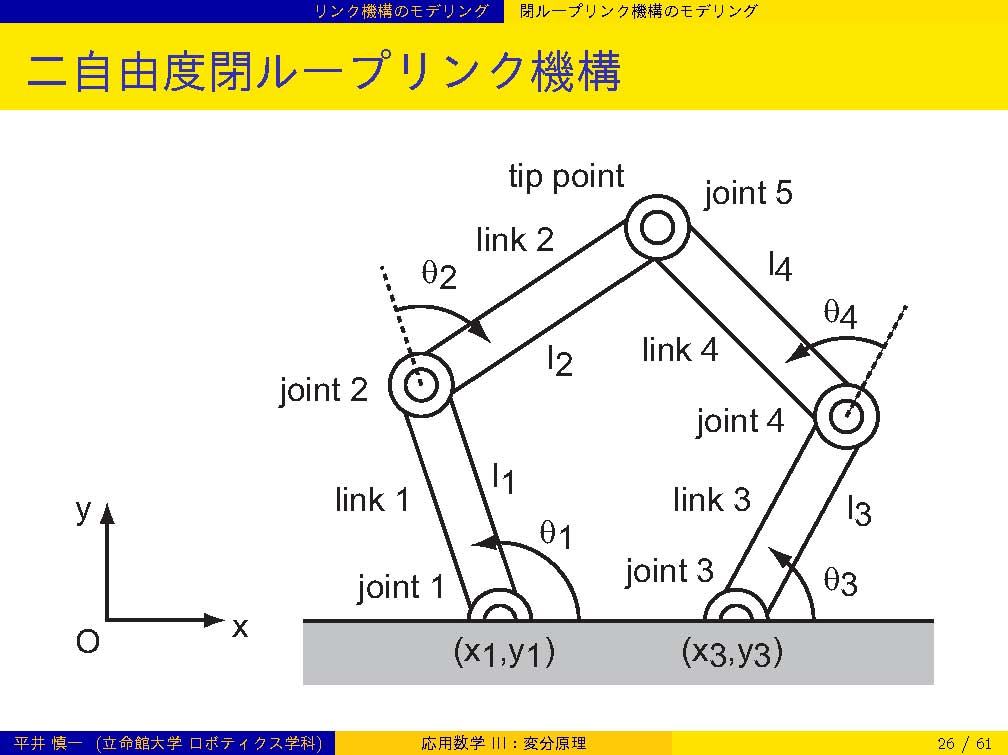
| 第9週 | 6/ 4 | 変分原理: 開ループ機構のモデリング,閉ループ機構のモデリング | |
| 第10週 | 6/11 | 変分原理: 剛体の回転運動,四元数 | |
| 第11週 | 6/18 | (小テスト) 射影,補間,変分原理 | |
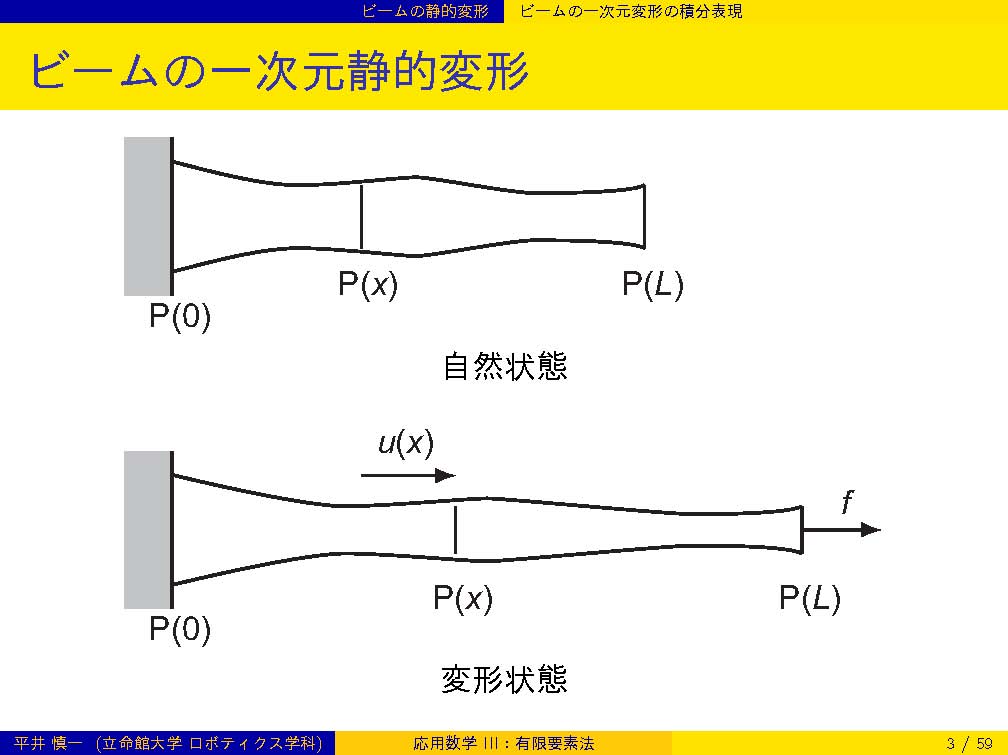
| 第12週 | 6/25 | 有限要素法: 形状関数,剛性行列,ビームの静的変形 | |
| 第13週 | 7/ 2 | 有限要素法: 慣性行列,ビームの動的変形 | |
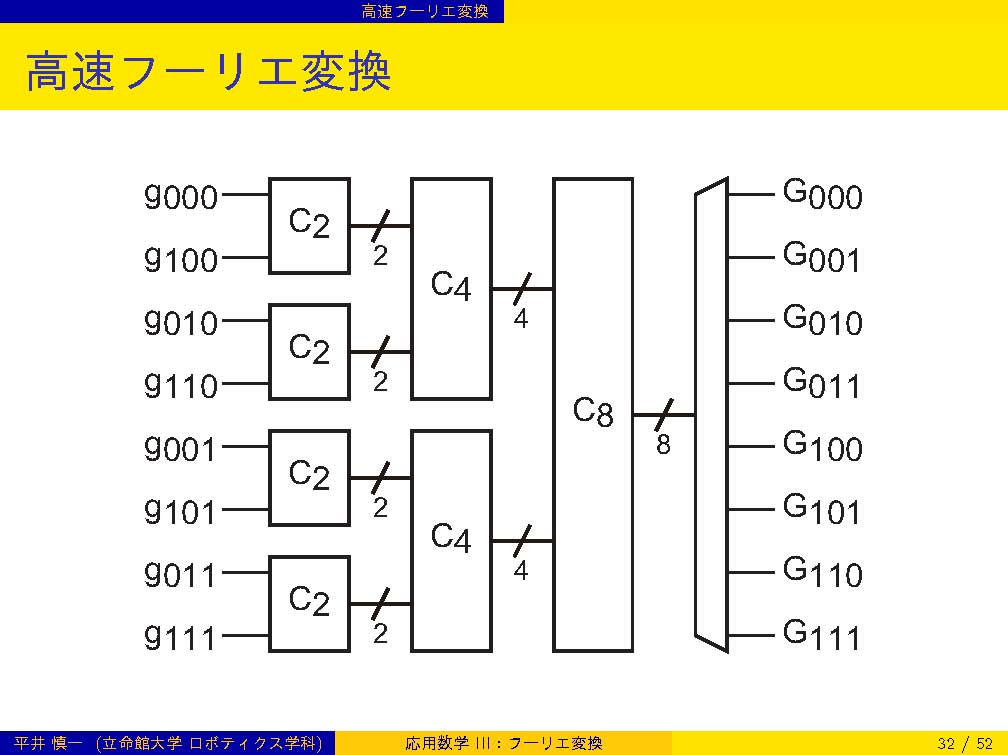
| 第14週 | 7/ 9 | フーリエ変換: 離散フーリエ変換(DFT),高速フーリエ変換(FFT) | |
| 第15週 | 7/16 | フーリエ変換: マッチドフィルタ,位相限定相関法 | |
| 第16週 | 7/30 | (試験) |
| 第1週 数値計算とは (2012.3.5更新) | 縮小版 | |
| 第2,3週 常微分方程式 (2012.4.13更新) (2012.3.5更新) | 縮小版 | |
| 第4週 連立一次方程式 (2012.4.13更新) (2012.3.16更新) | 縮小版 | |
| 第5,6週 射影 (2012.6.22更新) (2012.3.21更新) | 縮小版 | |
| 第7週 補間 (2012.4.13更新) (2012.3.23更新) | 縮小版 | |
| 第8,9,10週 変分原理 (2012.6.12更新) (2012.6.11更新) (2012.3.23更新) | 縮小版 | |
| 第11,12,13週 有限要素法 (2012.7.2更新) (2012.6.29更新) (2012.3.26更新) | 縮小版 | |
| 第14,15週 フーリエ変換 (2012.7.16更新) (2012.6.20更新) | 縮小版 | |
| 機械システム学のための数値計算法 (第2刷) 正誤表 (2012.7.4更新) |








|
| 評価: | 定期試験60% 小テスト40% |
| 教科書: | 機械システム学のための数値計算法 (第2刷) |
| ISBN 978-4-339-06094-2 | |
| 正誤表 | |
| 参考書: | Linear Algebra and Its Applications |
| Gilbert Strang Thomson Learning ISBN 0-15-551005-3 | |
| 訳書 線形代数とその応用 山口,井上訳 産業図書 ISBN 978-4782805022 | |
| 信号処理論 (ロボティクスシリーズ 4) | |
| 牧川 方昭 コロナ社 ISBN:978-4-339-04515-4 |
| 常微分方程式 | |
| 連立一次方程式 | |
| 射影 | |
| 補間 |