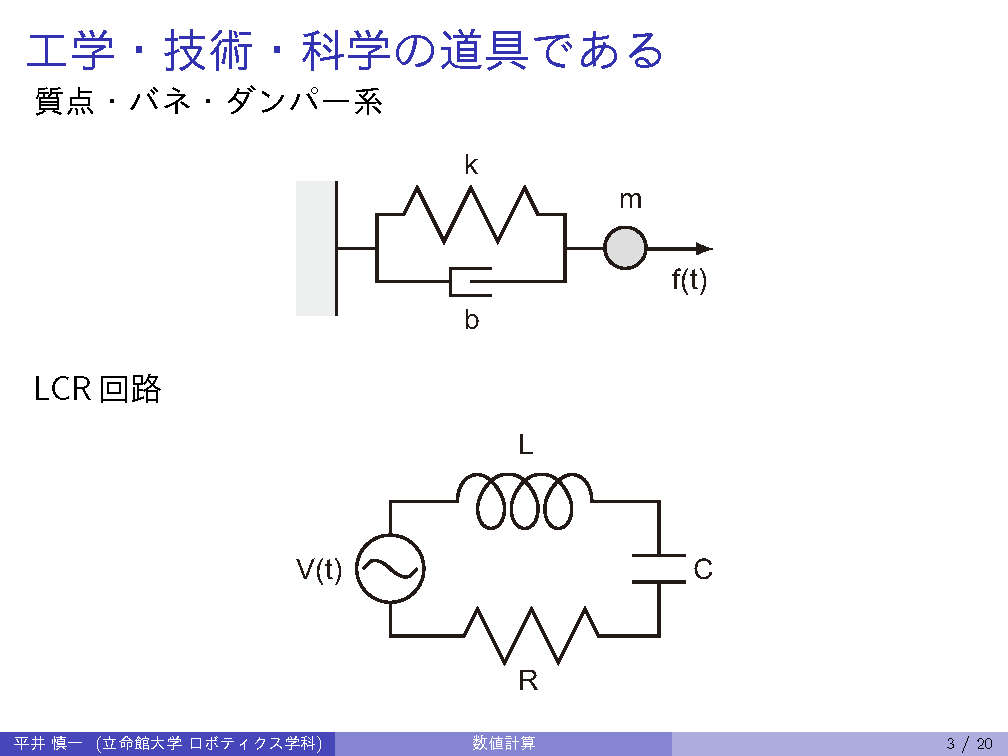
Provides fundamental numerical algorithms including numerical solution of ordinary differential equations, linear computations, projection matrices, and finite element method. Students will write programs on these topics to understand and to use practically the algorithms. (Dept. Mechanical Eng. / Robotics, B3)
|
1st |
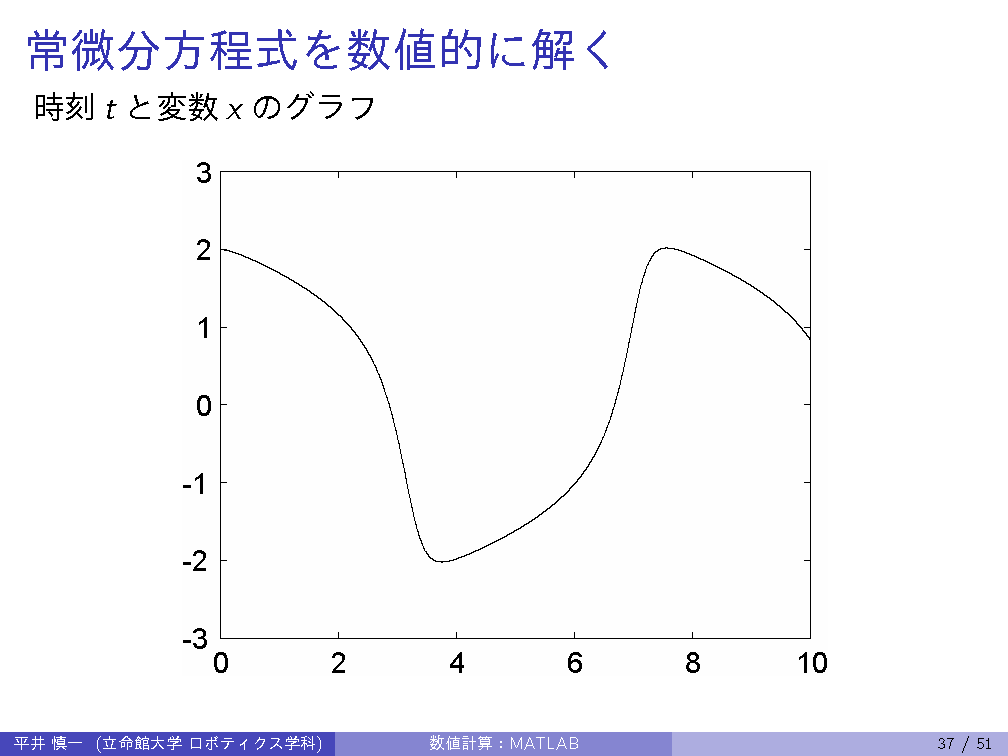
4/10 | Introduction: Analytical solution, Numerical solution |
| 2nd | 4/17 | MATLAB: matrices and vectors, ODE solver, graphs |
| 3rd | 4/24 | MATLAB: optimization, parameters, random numbers |
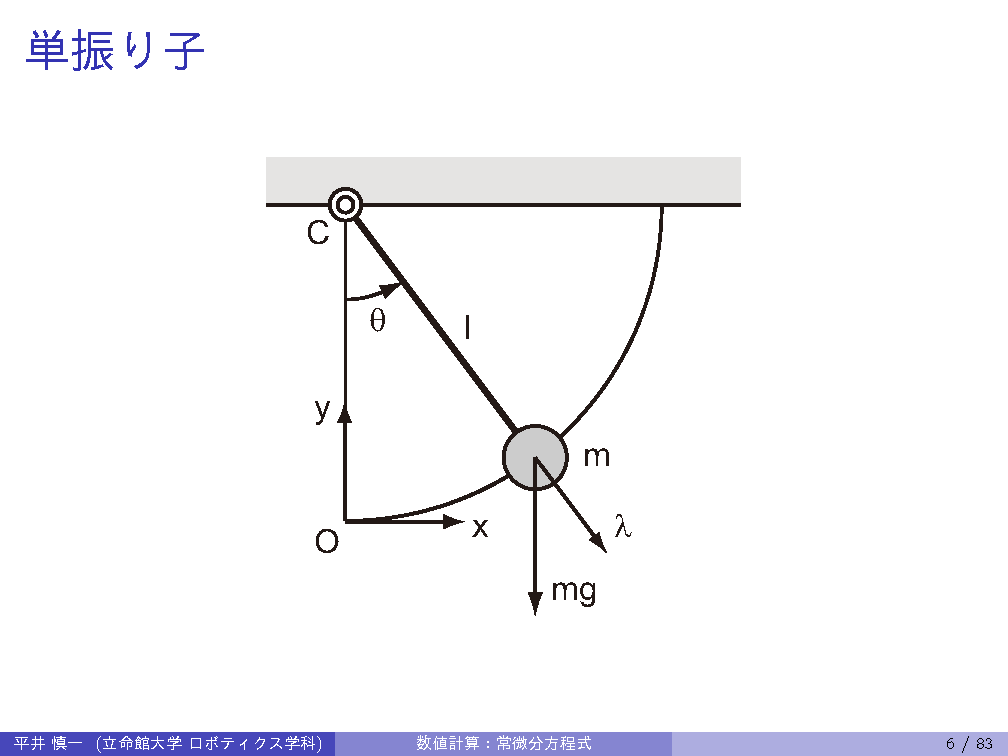
| 4th | 5/ 1 | ODE: canonical forms of ordinary differential equations, state variables, Runge-Kutta method |
| 5th | 5/ 8 | ODE: Runge-Kutta-Fehlberg method, constraints, constraint stabilization method |
| 6th | 5/15 | Linear equations: LU decomposition, pivoting LU decomposition |
| 7th | 5/22 | Linear equations: pivot selecting LU decomposition, Cholesky decomposition |
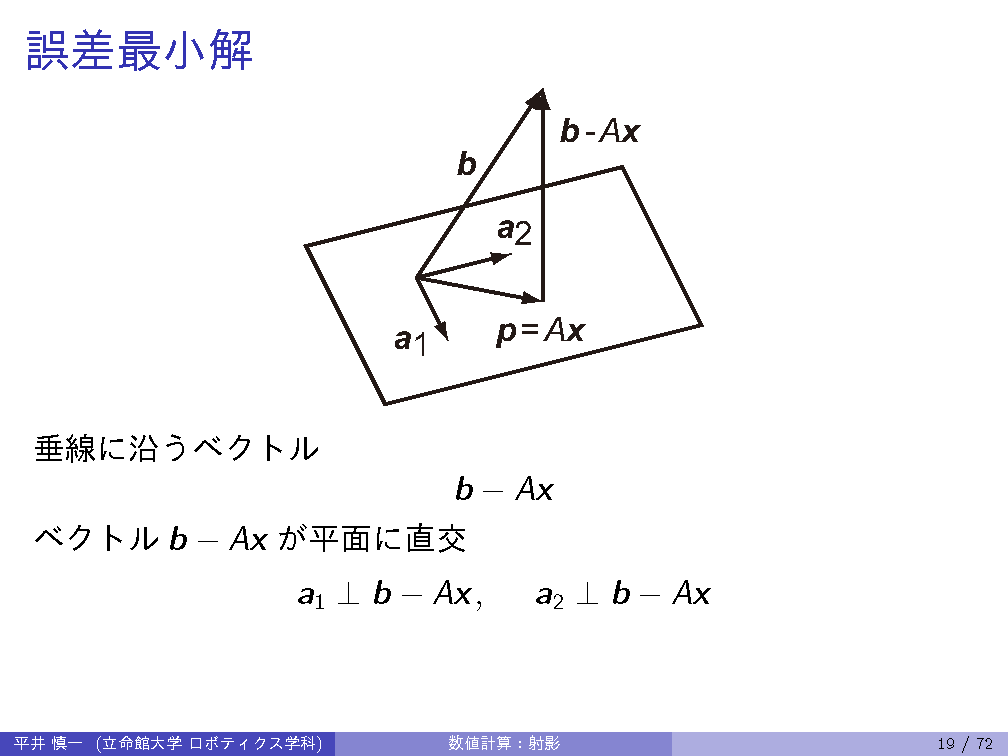
| 8th | 6/ 5 | Projection: projection matrix, Gram-Schmidt orthogonalization, QR decomposition |
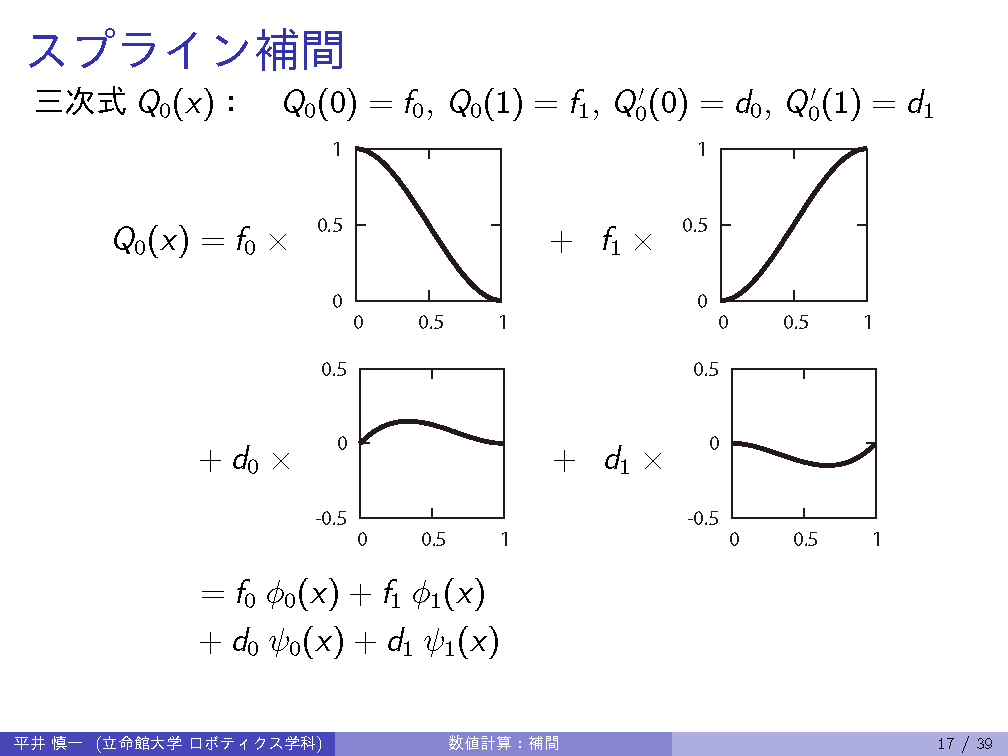
| 9th | 6/12 | Interpolation: piecewise linear interpolation, spline interpolation |
| 10th | 6/19 | Probabilistic algorithm: random numbers, uniform random numbers, normal random numbers |
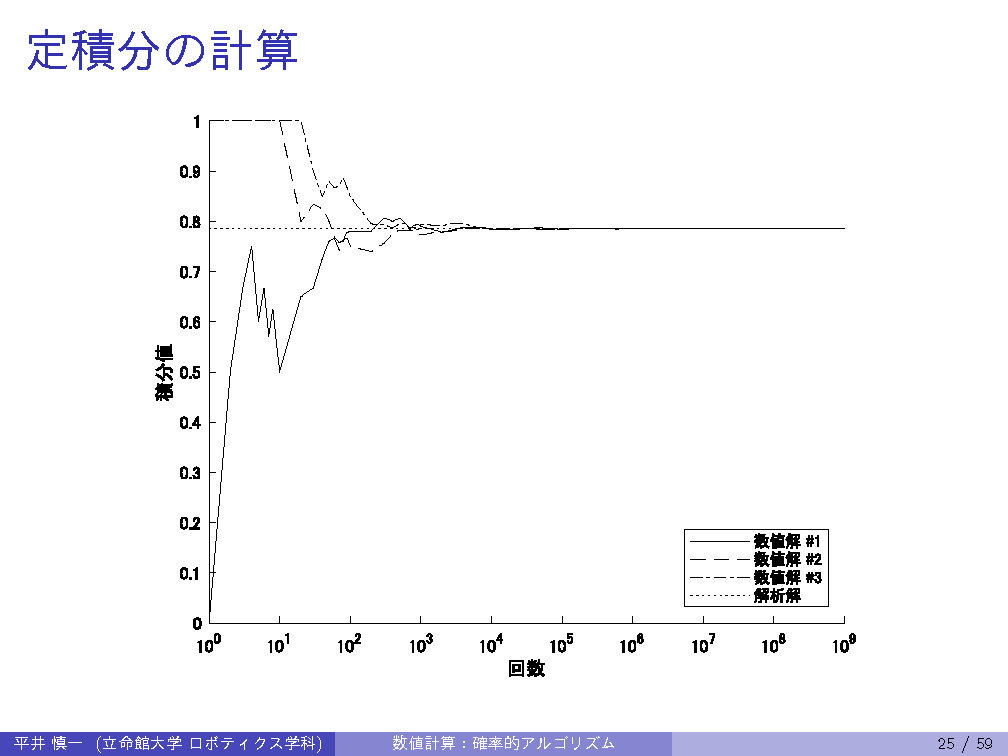
| 11th | 6/26 | Probabilistic algorithm: Monte Carlo method |
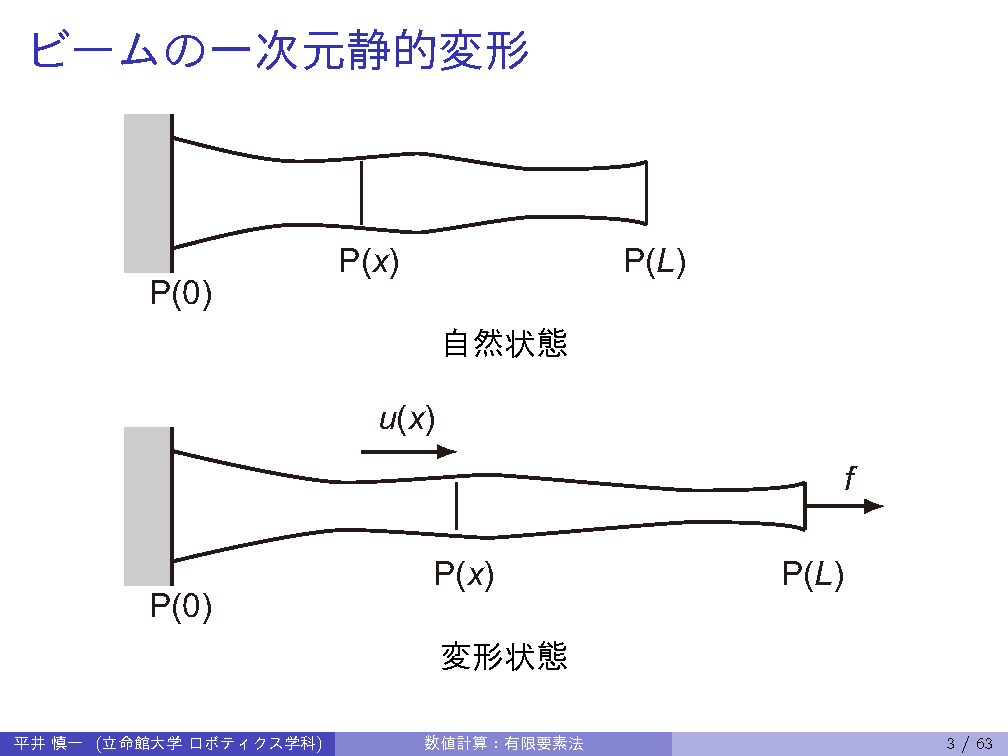
| 12th | 7/ 3 | FEM: shape functions, stiffness matrix, static deformation of beam |
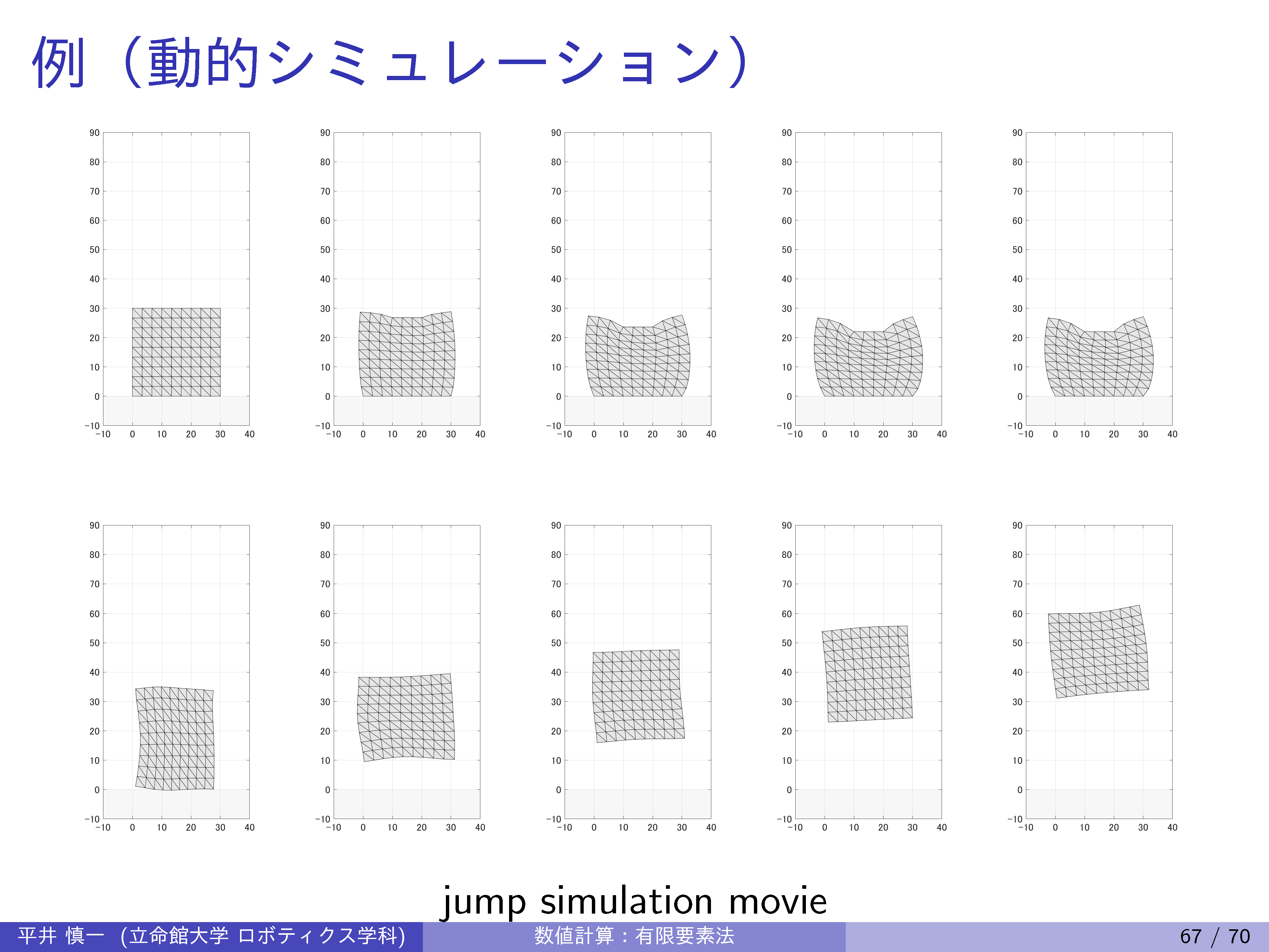
| 13th | 7/ 8 | FEM: inertia matrix, dynamic deformation of beam |
| 14th | 7/10 | FEM: 2D/3D inertia matrix, 2D/3D stiffness matrix |
| 15th | 7/17 | FEM: 2D/3D dynamic deformation |